Most az áll előttünk, hogy elosszuk a további tananyagot a különböző osztályokra.

Ekkor ugye tisztában kell lennünk azzal, hogy a kilencedik életév felé, tehát a harmadik iskolaévben kezdünk foglalkozni az állatokkal, megfelelő válogatásban, és mindig kapcsolatba hozzuk őket az emberrel, úgy, ahogy azt néhány próbán bemutattam.[1]

Ezt folytatjuk azután a negyedik iskolaévben, így tehát a harmadik és a negyedik iskolaévben az állatvilágot tesszük természettudományos módon vizsgálódásunk tárgyává az emberrel való kapcsolatában.

Aztán az ötödik iskolaévben arra térünk rá, hogy ismeretlenebb állatokat fűzünk még hozzá, de ebben az ötödik iskolaévben kezdünk el foglalkozni a növénytannal is, és ezt azután kifejezetten úgy műveljük, ahogy azt megbeszéltük a szemináriumunk didaktikai részében.

A hatodik iskolaévben, folytassuk a növénytant, és térjünk rá az ásványokkal való foglalkozásra. Az ásványokkal való foglalkozásnak azonban mindenképpen a földrajzzal összefüggésben kell történnie.

A hetedik iskolaévben megint csak térjünk vissza az emberhez, és különösen azt próbáljuk meg megtanítani, amire tegnap utaltam,[2] amit a táplálkozás illetve az egészség viszonyairól meg kellene tanítanunk az embernek. És próbáljunk meg annak a segítségével, amit fizikai és kémiai fogalmakban nyerünk, összefüggő szemléltetést adni a foglalkoztatottsági illetve termelési viszonyokról - vagyis valamilyen üzemről - és a közlekedési viszonyokról; mindezt összefüggésben a fizika, a kémia és a földrajz tanításával, a természetrajzból kiindulva.

A nyolcadik iskolaévben úgy kell majd felépíteniük az embert, hogy bemutatják azt, ami kívülről beléje épül: a csontok mechanikáját, az izomzat mechanikáját, a szem belső felépítését és így tovább. Azután most megint csak adnak egy összefüggő szemléltetést a termelési és közlekedési viszonyokról, összefüggésben a fizikával, a kémiával és a földrajzzal.

Ha lényegét tekintve úgy alakítják a természetismereti oktatást, ahogy éppen megbeszéltük, akkor igen élettelivé tudják tenni majd, és a természetismeretből kiindulva fel fogják ébreszteni a gyermek érdeklődését minden világi és minden emberi dolog iránt.

A fizika tanítását a hatodik iskolaévben kezdjük el, mégpedig úgy, hogy éppenséggel ahhoz kapcsoljuk, amit a gyerekek a zenetanításból nyertek. Azzal kezdjük a fizikatanítást, hogy a zenéből kibontjuk az akusztikát. Tehát az akusztikát éppenséggel a zenei hangtanhoz kapcsoljuk, s azután rátérünk az emberi gégefő fizikai-fiziológiai sajátságainak megbeszélésére. Az emberi szemet ekkor még nem vizsgálhatjuk, de a gégefőről beszélhetünk. Azután rátérünk - minthogy csupán a legfontosabb dolgokat vesszük át - az optikára és a hőtanra. Az elektromosság és a mágnesesség alapfogalmaival is ebben a hatodik iskolaévben foglalkozunk.

Azután a hetedik iskolaévben kibővítjük az ismereteket az akusztikáról, a termodinamikáról, vagyis a hőtanról, az optikáról, az elektromosságról és a mágnesességről. És csak innen indulva térünk rá a legfontosabb mechanikai alapfogalmakra, mint az emelő, a kútkerék, a görgő, a csigasor, a görgősor, a lejtő, a henger, a csavar és így tovább.

Azután egy olyan folyamatból indulunk ki, mint az égés, és átmenetet keresünk ettől a mindennapos folyamattól az egyszerű kémiai fogalmakhoz.

A nyolcadik iskolaévben azután ismételten kibővítjük azt, amivel a hatodik évben foglalkoztunk, és rátérünk a hidraulikára, vagyis a vízben ható erők tanára. Vagyis mindazokkal a dolgokkal foglalkozunk, ami olyan fogalmakhoz kapcsolódik, mint a víz oldalnyomása, a felhajtóerő: minden, ami az archimédeszi alapelvhez, vagyis a hidraulika területére tartozik.

Szép lett volna három éven át előadásokat tartani itt a pedagógiáról, és minden egyes olyan dologgal, amelyet saját tapasztalataik alapján kell kialakítaniuk, alappéldákon keresztül is foglalkozni. Ez azonban nem lehetséges. Így hát meg kell elégednünk azzal, amit sikerült itt bemutatnunk.

Azután bizonyos értelemben lezárjuk a fizikatanítást az aerodinamikával, tehát a levegő mechanikájával, amikor is minden szóba kerül, ami összefügg a klimatológiával, a barométerrel illetve az időjárástannal.

És tovább vezetjük az egyszerű kémiai fogalmakat, hogy így a gyermek azt is megtanulja megérteni, hogyan függenek össze az ipari folyamatok a kémiai folyamatokkal. Megpróbáljuk a kémiai fogalmakkal összefüggésben levezetni azt, amit el kell mondanunk azokra az anyagokra vonatkozóan, amelyek a szerves testet felépítik: a keményítők, a cukrok, a fehérjék, a zsírok.

Most az lesz a dolgunk, hogy azt is elosszuk a nyolc osztályra, ami a számolásra, a matematikára, a geometriára vonatkozik.

Tudják ugye, hogy a külső metodika előírja, hogy az első iskolaévben első sorban a százas számkörig terjedően kell foglalkozni a számokkal. Tarthatjuk is magunkat ehhez, hiszen tulajdonképpen mindegy, ha az egyszerű számoknál maradunk, hogy mennyire bővítjük ki a számkört az első iskolaévben. Az a lényeg, hogy amilyen széles számkörben dolgoznak, azon belül úgy alkalmazzák a számolási műveleteket, hogy legyenek tekintettel arra, amit mondtam.[3] az összeadást előbb az összegből kiindulva, a kivonást a maradékból kiindulva, a szorzást a szorzatból kiindulva, az osztást pedig a hányadosból kiindulva vezessék le. Vagyis épp ellenkezőleg, mint ahogy szokásosan teszik. És csak miután megmutattuk, hogy 5 az 3 meg 2, akkor mutatjuk meg a fordítottját: 2 és 3 összeadásával 5-öt kapunk. Mert erős képzeteket kell életre hívnunk a gyermekben arról, hogy 5 egyenlő 3 meg 2-vel, hogy viszont 5 az 4 meg 1-gyel is egyenlő, és így tovább. Tehát az összeadás csupán másodikként következik az összeg felosztása után; a kivonás pedig az után, hogy megkérdeztük: mit kell kivonnom egy adott kisebbítendőből, hogy egy bizonyos maradékot kapjak, és így tovább. Ahogy mondtam: hogy ezt akkor az egyszerű számokkal végezzük az első iskolaévben, az magától értetődik. Hogy azonban most 100-ig vagy 105- ig vagy 95-ig terjedő számkört használunk-e, ez alapjában véve mellékes dolog.

Ahogy viszont a gyermek túl van a fogváltáson, mindjárt el kell kezdenünk megtanultatni vele az egyszeregyet, s tőlem akár az „egymegegyet” is; legalábbis mondjuk a hatos vagy hetes számig. Tehát lehetőleg korán tanultassuk meg a gyermekkel emlékezetből az egyszeregyet és az „egymegegyet”, miután csupán lényegileg elmagyaráztuk neki, mi is ez tulajdonképpen, lényegileg elmagyaráztuk neki az egyszerű szorzás példáján, amelyet úgy ragadunk meg, ahogy azt elmondtuk. Vagyis alighogy megvan a lehetőségünk, hogy megtanítsuk a gyermeknek a szorzás fogalmát, máris ruházzuk rá azt a kötelességét, hogy emlékezetből megtanulja az egyszeregyet.

Azután a második iskolaévben vezessük tovább a számolási műveleteket egy nagyobb számkörben. Próbáljunk meg egyszerűbb feladatokat leírás nélkül is, fejben ugyebár, szóban elvégezni a diákjainkkal. A meg nem nevezett számokkal való munkát lehetőleg először tárgyakkal próbáljuk meg bevezetni - elmondtam ugye önöknek, hogyan vezethetik be babszemekkel vagy bármivel a meg nem nevezett számokat. Viszont persze nem szabadna szem elől tévesztenünk a megnevezett számokkal összefüggő számolást sem.

A harmadik iskolaévben komplikáltabb számokkal folytatunk mindent, és a négy alapműveletet, ahogy a második évben dolgoztunk velük, már a gyakorlati élet bizonyos egyszerű dolgaira is alkalmazzuk.

A negyedik iskolaévben folytatjuk mindazt, amivel az első iskolaévekben foglalkoztunk. De most rá kell térnünk a törtekre, és főként a tizedes törtekre.

Az ötödik iskolaévben azután folytatni kívánjuk a törtekkel és a tizedes törtekkel való foglalkozást, és mindazt közel hozzuk a gyermekhez, ami megadja neki annak a képességét, hogy egész, tört, illetve tizedes tört alakban kifejezett számok között szabadon számolva mozoghasson.

Azután a hatodik iskolaévben térjünk rá a kamat- illetve százalékszámításra, a leszámítolásra az egyszerű váltószámításra, és alapozzuk meg ezzel a betűkkel való számolást, ahogy azt bemutattuk.

Most kérem, vegyük tekintetbe, hogy a hatodik iskolaévig a geometriai formákat: a kört, a háromszöget és így tovább, kibontottuk a rajzolásból, miután az első években először az írástanítás céljaira használtuk a rajzolást. Ezután fokozatosan arra tértünk rá, hogy abból a rajzolásból, amelyet az írástanítás érdekében műveltünk, komplikáltabb formákat vezettünk le a gyermeknek, amelyek önmaguk kedvéért, a rajzolás kedvéért készültek; és festettünk is, csupán a festés öröméért. Ebbe a szférába vezetjük a rajz- és festéstanítást a negyedik iskolaévben, és a rajzban megtanítjuk, mi is egy kör, egy ellipszis és így tovább. A rajzolásból kiindulva tanítjuk meg ezeket. Tovább is megyünk itt még, éppenséggel mindig is plasztikus formákhoz eljutva, amikor a plasztilinnel dolgozunk - ha hozzá tudunk jutni; egyébként használhatunk bármi mást, és még ha sár volna az utcáról, az sem baj! -, hogy a formalátást, a formaérzéket is kialakítsuk.

Abból, amit ily módon megtanítottunk a rajzban, a matematikatanítás, a geometriatanítás most átveszi azt, amit a gyerekek tudnak. Most térünk csak rá arra, hogy geometriai szempontból elmagyarázzuk, mi is egy háromszög, egy négyzet, egy kör és így tovább. Tehát a formák térbeli felfogását a rajzolásból vezetjük le. És amit a gyerekek a rajzban megtanultak, ahhoz csak most, a hatodik iskolaévben közelítsünk geometriai fogalmakkal. Látni fogjuk, hogy azután cserébe valami mást veszünk majd fel a rajzolásba.

A hetedik iskolaévben próbáljuk meg, miután áttértünk a betűkkel való számolásra, megtanítani a hatványozást és a gyökvonást; és azt is, amit pozitív és negatív számokkal való számolásnak neveznek. És mindenekelőtt próbáljuk meg bevezetni a gyerekeket abba, amit a gyakorlati élet szabad alkalmazásaihoz kapcsolódóan az egyenletek tanának nevezhetünk.

Azután folytassuk a nyolcadik iskolaévben azt, ami az egyenletek tanával összefügg, ameddig el tudjuk juttatni a gyerekeket, és kapcsoljunk hozzá kerület- illetve területszámításokat, és a geometriai felület tanát, ahogy azt tegnap legalábbis érintettük.

Ez képet ad önöknek arról, hogyan is járjanak el a matematikában és a geometriában a gyerekekkel.

Nos, amint láttuk, az első iskolai években úgy végezzük a rajztanítást, hogy előbb egy bizonyos érzéket adunk a gyermeknek a kerek, szögletes stb. formákról.

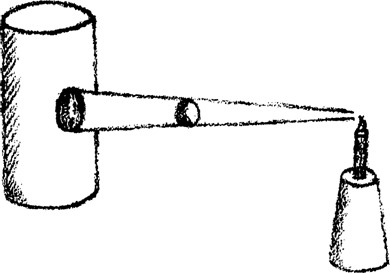
A formákból kiindulva vezetjük le azt, amire azután az írás tanításánál szükségünk lesz. Ennek az elemi rajztanításnak a kezdetén teljesen kerüljük azt, hogy bármit is utánozzunk. Kerüljék el, amennyire csak tudják, hogy a gyermekkel először egy széket, egy virágot vagy bármi mást utánoztassanak a rajzban, inkább amennyire csak tudnak, hozakodjanak elő nekik önmagukból kibontott vonalas formákkal: kerek, hegyes, félkörös, elliptikus, egyenes formákkal és így tovább. Ébresszék fel a gyermekben az érzést, hogy micsoda különbség is van a kör görbülete illetve az ellipszis görbülete között. Röviden: ébresszék fel a formaérzéket, mielőtt az utánzás ösztöne felébred! Amit a formákban ápoltunk, azt csupán később alkalmaztassák az utánzásban. Rajzoltassanak előbb egy szöget a gyermekkel, hogy felfogja a formában a szög mibenlétét. Azután mutassák meg neki a széket, és mondják: „Látod, itt van egy szög, és itt van egy másik szög” (geometriai értelemben vett szögekről van szó - a ford. megj.) és így tovább. Semmit se másoltassanak le a gyermekkel, még mielőtt belső érzékből kiindulva önállóságában nem ápolták benne a formát, amelyet azután később majd utánozni is lehet. És ezt még akkor is tartsák meg, amikor áttérnek a rajzolással, a festéssel és a térplasztikával való önállóbb foglalkozáshoz.

Azután a hatodik iskolaévben vezessék be az egyszerű vetítés- és árnyéktant, amelyet szabad kézzel is alkalmaznak, illetve vonalzóval, körzővel és más eszközökkel is. Figyeljenek oda arra, hogy a gyermeknek jó fogalma legyen róla és le tudja rajzolni, modellezni tudja, ha mondjuk itt van egy henger, itt pedig egy golyó, és a golyót megvilágítja egy fényforrás, hogy néz ki a golyó árnyéka a hengeren. Hogy hogyan vetülnek az árnyékok!

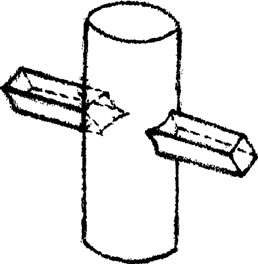
A hatodik iskolaévben tehát meg kell jelennie az egyszerű vetítés- és árnyéktannak. A gyermeknek képet kell kapnia arról, hogyan vetülnek az árnyékok sík felületre, hajlított felületekre, képet kell kapnia különféle egyéb többé-kevésbé sík alakzatokról vagy testekről, és tudnia kell ezeket lerajzolni, modellezni. A gyermeknek ebben a hatodik iskolaévben már fogalmat kell alkotnia arról, hogyan kapcsolódnak össze a technikai dolgok a szépséggel, hogyan lehet egy szék egyszerre technikailag alkalmas egy funkció betöltésére, és hogyan lehet emellett szép formája. És a technika összekapcsolásának a szépséggel fogalommá kell válnia a gyermekben (mintegy „meg kell ragadni” azt), így kell megtanulnia alkalmazni.

Azután a hetedik iskolaévben mindazon dolgokkal kellene foglalkozni, amelyek az áthatolásokra vonatkoznak. Egyszerű példaként tehát azt mondják: itt van egy henger, ezen keresztülhatol egy szögletes rúd. Tehát a szögletes rudat áttoljuk a hengeren. Meg kell mutatniuk, hogy milyen vágási felület keletkezik ekkor a hengeren a behatolásnál és az újbóli kifelé áthatolásnál.

Ezt meg kell tanulnia a gyermeknek. Ilyen dolgokat kell megtanulnia, hogy mi keletkezik, ha testek vagy felületek kölcsönösen áthatolnak egymáson, hogy így tudja, mi a különbség aközött, ha egy kályhacső egyenesen megy keresztül fent a plafonon, amikor kör formájú áthatolási felület keletkezik, illetve aközött, ha ferdén megy keresztül, amikor is ellipszis formájú áthatolási felület keletkezik. Azután jó képet kell kapnia a gyermeknek ebben az évben a perspektívahatásról. Tehát az egyszerű perspektivikus rajzról, a rövidülésről a távolabbi dolgok esetében, a nyúlásról a közelebbi dolgok esetében, az átfedésekről és így tovább. És azután megint csak a technika összekapcsolásáról a szépséggel, hogy így a gyermeknek elképzelése legyen arról, hogy az vajon szépe vagy pedig kellemetlen hatású, csúnya, ha valahogy, mondjuk egy kiugrás által, részleges takarás keletkezik a ház egyik falán. Egy ilyen kiugrás széppé vagy csúnyává is tehet egy falat. Az ilyen dolgok nagyon erősen hatnak, ha pont a hetedik iskolaévben, vagyis 13-14 éves korában tanítjuk meg őket a gyermeknek.

Mindezeket művészi szintre fokozzuk, amikor a nyolcadik iskolaév felé járunk.

És hasonló módon, ahogy ezekkel a dolgokkal foglalkoztunk, kell most a fennmaradó dolgokkal is foglalkoznunk. Ma délután majd visszatérünk erre, és kiegészítésképpen hozzá kell majd fűznünk egyet s mást a tantervünkhöz. Mindenekelőtt arra kell majd odafigyelnünk, hogyan kell az első iskolaévben a zenei dolgokat is lehetőleg az egyszerű, elementáris dolgokból levezetnünk, és hogyan térünk rá azután a bonyolultabb részekre körülbelül a harmadik iskolaévtől kezdődően. Így hát a gyermek a hangszernél - és szó szerint a hangszer mellett - és az éneklésből is fokozatosan beépíti magába azt, ami éppen alakítóan, kiművelően hat képességeire.

Ki kell viszont emelni minden egyéb művészi tevékenységből a tornát és az euritmiát. A zenei részből, és a többi művészi tevékenységből is, ki kell emelni a tornát és az euritmiát.